题目
1.利用高斯公式计算曲面积分:-|||-(3) iint (x)^3dydz+2x(z)^2dzdx+3(y)^2zdxdy 其中∑为抛物面 =4-(x)^2-(y)^2 被平面 z=0 所-|||-截下的部分的下侧;

题目解答
答案
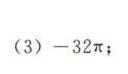
解析
步骤 1:确定积分区域
抛物面 $z=4-{x}^{2}-{y}^{2}$ 被平面 $z=0$ 所截下的部分是一个以原点为中心,半径为2的圆盘,其在 $z=0$ 平面上的投影为 $x^2+y^2\leq4$。由于积分区域是抛物面的下侧,因此积分区域为 $0\leq z\leq 4-x^2-y^2$。
步骤 2:应用高斯公式
高斯公式(散度定理)表明,对于一个闭合曲面S,其上的向量场F的通量等于该向量场在闭合曲面S所围成的体积V内的散度的积分。即
$$\iint_{S} \mathbf{F} \cdot d\mathbf{S} = \iiint_{V} \nabla \cdot \mathbf{F} \, dV$$
其中,$\mathbf{F} = (x^3, 2xz^2, 3y^2z)$,$\nabla \cdot \mathbf{F} = \frac{\partial}{\partial x}(x^3) + \frac{\partial}{\partial y}(2xz^2) + \frac{\partial}{\partial z}(3y^2z) = 3x^2 + 3y^2$。
步骤 3:计算体积积分
根据高斯公式,原曲面积分可以转化为体积积分:
$$\iiint_{V} (3x^2 + 3y^2) \, dV$$
其中,$V$ 是由抛物面 $z=4-x^2-y^2$ 和平面 $z=0$ 围成的体积。为了方便计算,我们采用柱坐标系,其中 $x=r\cos\theta$,$y=r\sin\theta$,$z=z$,$dV=r\,dr\,d\theta\,dz$。积分区域为 $0\leq r\leq 2$,$0\leq \theta\leq 2\pi$,$0\leq z\leq 4-r^2$。因此,体积积分为:
$$\int_{0}^{2\pi} \int_{0}^{2} \int_{0}^{4-r^2} (3r^2) r\,dz\,dr\,d\theta = \int_{0}^{2\pi} \int_{0}^{2} 3r^3(4-r^2) \,dr\,d\theta$$
$$= \int_{0}^{2\pi} \int_{0}^{2} (12r^3 - 3r^5) \,dr\,d\theta = \int_{0}^{2\pi} \left[3r^4 - \frac{3}{6}r^6\right]_{0}^{2} \,d\theta$$
$$= \int_{0}^{2\pi} \left(3\cdot2^4 - \frac{1}{2}\cdot2^6\right) \,d\theta = \int_{0}^{2\pi} (48 - 32) \,d\theta = 16\int_{0}^{2\pi} \,d\theta = 16\cdot2\pi = 32\pi$$
由于积分区域是抛物面的下侧,因此最终结果为 $-32\pi$。
抛物面 $z=4-{x}^{2}-{y}^{2}$ 被平面 $z=0$ 所截下的部分是一个以原点为中心,半径为2的圆盘,其在 $z=0$ 平面上的投影为 $x^2+y^2\leq4$。由于积分区域是抛物面的下侧,因此积分区域为 $0\leq z\leq 4-x^2-y^2$。
步骤 2:应用高斯公式
高斯公式(散度定理)表明,对于一个闭合曲面S,其上的向量场F的通量等于该向量场在闭合曲面S所围成的体积V内的散度的积分。即
$$\iint_{S} \mathbf{F} \cdot d\mathbf{S} = \iiint_{V} \nabla \cdot \mathbf{F} \, dV$$
其中,$\mathbf{F} = (x^3, 2xz^2, 3y^2z)$,$\nabla \cdot \mathbf{F} = \frac{\partial}{\partial x}(x^3) + \frac{\partial}{\partial y}(2xz^2) + \frac{\partial}{\partial z}(3y^2z) = 3x^2 + 3y^2$。
步骤 3:计算体积积分
根据高斯公式,原曲面积分可以转化为体积积分:
$$\iiint_{V} (3x^2 + 3y^2) \, dV$$
其中,$V$ 是由抛物面 $z=4-x^2-y^2$ 和平面 $z=0$ 围成的体积。为了方便计算,我们采用柱坐标系,其中 $x=r\cos\theta$,$y=r\sin\theta$,$z=z$,$dV=r\,dr\,d\theta\,dz$。积分区域为 $0\leq r\leq 2$,$0\leq \theta\leq 2\pi$,$0\leq z\leq 4-r^2$。因此,体积积分为:
$$\int_{0}^{2\pi} \int_{0}^{2} \int_{0}^{4-r^2} (3r^2) r\,dz\,dr\,d\theta = \int_{0}^{2\pi} \int_{0}^{2} 3r^3(4-r^2) \,dr\,d\theta$$
$$= \int_{0}^{2\pi} \int_{0}^{2} (12r^3 - 3r^5) \,dr\,d\theta = \int_{0}^{2\pi} \left[3r^4 - \frac{3}{6}r^6\right]_{0}^{2} \,d\theta$$
$$= \int_{0}^{2\pi} \left(3\cdot2^4 - \frac{1}{2}\cdot2^6\right) \,d\theta = \int_{0}^{2\pi} (48 - 32) \,d\theta = 16\int_{0}^{2\pi} \,d\theta = 16\cdot2\pi = 32\pi$$
由于积分区域是抛物面的下侧,因此最终结果为 $-32\pi$。