题目
5.应用积分号下的积分法,求下列积分:-|||-(1) (int )_(0)^1sin (ln dfrac (1)(x))dfrac ({x)^b-(x)^a}(ln x)dx(bgt agt 0) ;-|||-(2) (int )_(0)^1cos (ln dfrac (1)(x))dfrac ({x)^b-(x)^a}(ln x)dx(bgt agt 0).

题目解答
答案
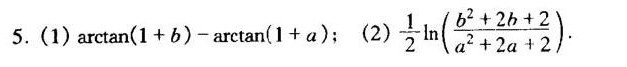
解析
步骤 1:引入积分号下的积分法
对于积分 ${\int }_{0}^{1}\sin (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{4}}{\ln x}dx$ 和 ${\int }_{0}^{1}\cos (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx$,我们可以通过引入积分号下的积分法来解决。首先,我们考虑一个更一般的积分形式 ${\int }_{0}^{1}\sin (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx$,其中 $b > a > 0$。
步骤 2:利用积分号下的积分法
我们考虑函数 $f(t) = {\int }_{0}^{1}\sin (\ln \dfrac {1}{x})\dfrac {{x}^{t}-{x}^{a}}{\ln x}dx$,其中 $t$ 是一个参数。我们注意到,当 $t=b$ 时,$f(b)$ 就是我们要计算的积分。为了计算 $f(t)$,我们首先计算 $f'(t)$,即对 $t$ 求导。
步骤 3:计算 $f'(t)$
对 $f(t)$ 关于 $t$ 求导,我们得到 $f'(t) = {\int }_{0}^{1}\sin (\ln \dfrac {1}{x}){x}^{t}dx$。这个积分可以通过变量替换 $u = \ln \dfrac {1}{x}$ 来计算。于是,$du = -\dfrac {1}{x}dx$,且当 $x$ 从 $0$ 到 $1$ 变化时,$u$ 从 $+\infty$ 到 $0$ 变化。因此,$f'(t) = {\int }_{+\infty}^{0}\sin u e^{-tu}(-du) = {\int }_{0}^{+\infty}\sin u e^{-tu}du$。这个积分可以通过分部积分法计算,得到 $f'(t) = \dfrac {1}{1+t^2}$。
步骤 4:计算 $f(t)$
由于 $f'(t) = \dfrac {1}{1+t^2}$,我们可以通过积分得到 $f(t) = \arctan(t) + C$,其中 $C$ 是积分常数。为了确定 $C$,我们注意到当 $t=a$ 时,$f(a) = 0$(因为 ${x}^{a}-{x}^{a}=0$)。因此,$C = -\arctan(a)$。所以,$f(t) = \arctan(t) - \arctan(a)$。
步骤 5:计算 $f(b)$
最后,我们计算 $f(b) = \arctan(b) - \arctan(a)$。因此,${\int }_{0}^{1}\sin (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx = \arctan(b) - \arctan(a)$。
步骤 6:计算 ${\int }_{0}^{1}\cos (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx$
对于 ${\int }_{0}^{1}\cos (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx$,我们采用类似的方法,得到 $f(t) = \dfrac {1}{2}\ln(1+t^2) + C$。通过同样的方法确定 $C$,我们得到 $f(t) = \dfrac {1}{2}\ln(1+t^2) - \dfrac {1}{2}\ln(1+a^2)$。因此,${\int }_{0}^{1}\cos (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx = \dfrac {1}{2}\ln(\dfrac {1+b^2}{1+a^2})$。
对于积分 ${\int }_{0}^{1}\sin (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{4}}{\ln x}dx$ 和 ${\int }_{0}^{1}\cos (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx$,我们可以通过引入积分号下的积分法来解决。首先,我们考虑一个更一般的积分形式 ${\int }_{0}^{1}\sin (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx$,其中 $b > a > 0$。
步骤 2:利用积分号下的积分法
我们考虑函数 $f(t) = {\int }_{0}^{1}\sin (\ln \dfrac {1}{x})\dfrac {{x}^{t}-{x}^{a}}{\ln x}dx$,其中 $t$ 是一个参数。我们注意到,当 $t=b$ 时,$f(b)$ 就是我们要计算的积分。为了计算 $f(t)$,我们首先计算 $f'(t)$,即对 $t$ 求导。
步骤 3:计算 $f'(t)$
对 $f(t)$ 关于 $t$ 求导,我们得到 $f'(t) = {\int }_{0}^{1}\sin (\ln \dfrac {1}{x}){x}^{t}dx$。这个积分可以通过变量替换 $u = \ln \dfrac {1}{x}$ 来计算。于是,$du = -\dfrac {1}{x}dx$,且当 $x$ 从 $0$ 到 $1$ 变化时,$u$ 从 $+\infty$ 到 $0$ 变化。因此,$f'(t) = {\int }_{+\infty}^{0}\sin u e^{-tu}(-du) = {\int }_{0}^{+\infty}\sin u e^{-tu}du$。这个积分可以通过分部积分法计算,得到 $f'(t) = \dfrac {1}{1+t^2}$。
步骤 4:计算 $f(t)$
由于 $f'(t) = \dfrac {1}{1+t^2}$,我们可以通过积分得到 $f(t) = \arctan(t) + C$,其中 $C$ 是积分常数。为了确定 $C$,我们注意到当 $t=a$ 时,$f(a) = 0$(因为 ${x}^{a}-{x}^{a}=0$)。因此,$C = -\arctan(a)$。所以,$f(t) = \arctan(t) - \arctan(a)$。
步骤 5:计算 $f(b)$
最后,我们计算 $f(b) = \arctan(b) - \arctan(a)$。因此,${\int }_{0}^{1}\sin (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx = \arctan(b) - \arctan(a)$。
步骤 6:计算 ${\int }_{0}^{1}\cos (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx$
对于 ${\int }_{0}^{1}\cos (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx$,我们采用类似的方法,得到 $f(t) = \dfrac {1}{2}\ln(1+t^2) + C$。通过同样的方法确定 $C$,我们得到 $f(t) = \dfrac {1}{2}\ln(1+t^2) - \dfrac {1}{2}\ln(1+a^2)$。因此,${\int }_{0}^{1}\cos (\ln \dfrac {1}{x})\dfrac {{x}^{b}-{x}^{a}}{\ln x}dx = \dfrac {1}{2}\ln(\dfrac {1+b^2}{1+a^2})$。