题目
根据数列极限的定义证明: (1)lim _(narrow infty )dfrac (1)({n)^2}=0-|||-__; (2)lim _(narrow infty )dfrac (1)({n)^2}=0-|||-__; (3)lim _(narrow infty )dfrac (1)({n)^2}=0-|||-__ (4)lim _(narrow infty )dfrac (1)({n)^2}=0-|||-__.
根据数列极限的定义证明:
(1)
;
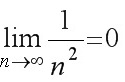(2)
;
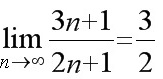(3)
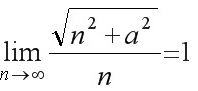
(4)
.
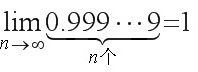题目解答
答案
证明(1)分析 要使
, 只须
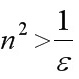, 即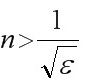
.
因为∀ε>0, ∃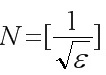
, 当n>N时, 有
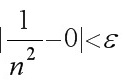, 所以.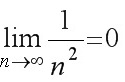
(2)分析 要使
, 只须
, 即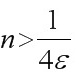
.
因为∀ε>0, ∃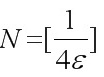
, 当n>N时, 有
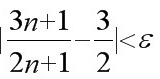, 所以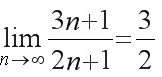
.
(3)分析 要使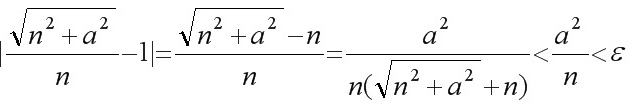
, 只须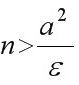
.
因为∀ε>0, ∃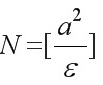
, 当∀n>N时, 有
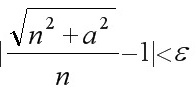, 所以.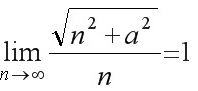
(4)分析 要使|0.99 ∙ ∙ ∙ 9-1|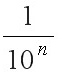
<ε , 只须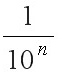<ε , 即
.
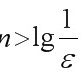因为∀ε>0, ∃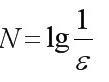
, 当∀n>N时, 有|0.99 ∙ ∙ ∙ 9-1|<ε , 所以.
解析
(1) 步骤 1：分析
要使$|\dfrac {1}{{n}^{2}}-0|=\dfrac {1}{{n}^{2}}\lt \varepsilon $, 只须${n}^{2}\gt \dfrac {1}{\varepsilon }$, 即$n\gt \dfrac {1}{\sqrt {\varepsilon }}$.
步骤 2：证明
因为∀ε>0, ∃$N=[ \dfrac {1}{\sqrt {\varepsilon }}] $, 当n>N时, 有$|\dfrac {1}{{n}^{2}}-0|\lt \varepsilon $, 所以$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}=0$.
(2) 步骤 1：分析
要使$\dfrac {3n+1}{2n+1}-\dfrac {3}{2}=\dfrac {1}{2(2n+1)}\lt \dfrac {1}{4n}\lt \varepsilon $, 只须$\dfrac {1}{4n}\lt \varepsilon $, 即$n\gt \dfrac {1}{4\varepsilon }$.
步骤 2：证明
因为∀ε>0, ∃$N=[ \dfrac {1}{4\varepsilon }] $, 当n>N时, 有$\dfrac {3n+1}{2n+1}-\dfrac {3}{2}|\lt \varepsilon $, 所以$\lim _{n\rightarrow \infty }\dfrac {3n+1}{2n+1}=\dfrac {3}{2}$.
(3) 步骤 1：分析
要使$\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n}-1=\dfrac {\sqrt {{n}^{2}+{a}^{2}}-n}{n}=\dfrac {{a}^{2}}{n(\sqrt {{n}^{2}+{a}^{2}}+n)}\lt \dfrac {{a}^{2}}{n}\lt \varepsilon $, 只须$n\gt \dfrac {{a}^{2}}{\varepsilon }$.
步骤 2：证明
因为∀ε>0, ∃$N=[ \dfrac {{a}^{2}}{\varepsilon }] $, 当∀n>N时, 有$\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n}-1|\lt \varepsilon $, 所以$\lim _{n\rightarrow \infty }\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n}=1$.
(4) 步骤 1：分析
要使|0.99 ∙ ∙ ∙ 9-1|$\dfrac {1}{{10}^{n}}$<ε , 只须$\dfrac {1}{{10}^{n}}$<ε , 即$n\gt \lg \dfrac {1}{\varepsilon }$.
步骤 2：证明
因为∀ε>0, ∃$N=\lg \dfrac {1}{\varepsilon }$, 当∀n>N时, 有|0.99 ∙ ∙ ∙ 9-1|<ε , 所以$\lim _{n\rightarrow \infty }0.999\cdots 9=1$ n→∞ n个.
要使$|\dfrac {1}{{n}^{2}}-0|=\dfrac {1}{{n}^{2}}\lt \varepsilon $, 只须${n}^{2}\gt \dfrac {1}{\varepsilon }$, 即$n\gt \dfrac {1}{\sqrt {\varepsilon }}$.
步骤 2：证明
因为∀ε>0, ∃$N=[ \dfrac {1}{\sqrt {\varepsilon }}] $, 当n>N时, 有$|\dfrac {1}{{n}^{2}}-0|\lt \varepsilon $, 所以$\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}=0$.
(2) 步骤 1：分析
要使$\dfrac {3n+1}{2n+1}-\dfrac {3}{2}=\dfrac {1}{2(2n+1)}\lt \dfrac {1}{4n}\lt \varepsilon $, 只须$\dfrac {1}{4n}\lt \varepsilon $, 即$n\gt \dfrac {1}{4\varepsilon }$.
步骤 2：证明
因为∀ε>0, ∃$N=[ \dfrac {1}{4\varepsilon }] $, 当n>N时, 有$\dfrac {3n+1}{2n+1}-\dfrac {3}{2}|\lt \varepsilon $, 所以$\lim _{n\rightarrow \infty }\dfrac {3n+1}{2n+1}=\dfrac {3}{2}$.
(3) 步骤 1：分析
要使$\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n}-1=\dfrac {\sqrt {{n}^{2}+{a}^{2}}-n}{n}=\dfrac {{a}^{2}}{n(\sqrt {{n}^{2}+{a}^{2}}+n)}\lt \dfrac {{a}^{2}}{n}\lt \varepsilon $, 只须$n\gt \dfrac {{a}^{2}}{\varepsilon }$.
步骤 2：证明
因为∀ε>0, ∃$N=[ \dfrac {{a}^{2}}{\varepsilon }] $, 当∀n>N时, 有$\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n}-1|\lt \varepsilon $, 所以$\lim _{n\rightarrow \infty }\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n}=1$.
(4) 步骤 1：分析
要使|0.99 ∙ ∙ ∙ 9-1|$\dfrac {1}{{10}^{n}}$<ε , 只须$\dfrac {1}{{10}^{n}}$<ε , 即$n\gt \lg \dfrac {1}{\varepsilon }$.
步骤 2：证明
因为∀ε>0, ∃$N=\lg \dfrac {1}{\varepsilon }$, 当∀n>N时, 有|0.99 ∙ ∙ ∙ 9-1|<ε , 所以$\lim _{n\rightarrow \infty }0.999\cdots 9=1$ n→∞ n个.