题目
例3.8 设二维随机变量 (X,Y)sim N((mu )_(1),(mu )_(2);({sigma )_(1)}^2,({sigma )_(2)}^2;rho ), 证明-|||-sim N(({M)_(1)}({O)_(1)}^2) , sim N((M)_(2),({O)_(2)}^2)
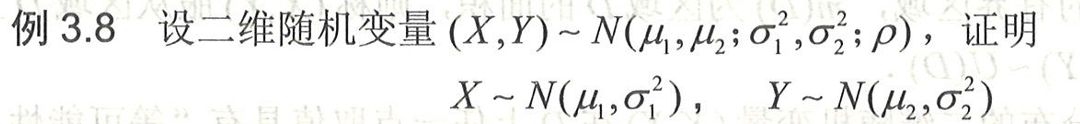
题目解答
答案

解析
步骤 1:确定联合密度函数
二维随机变量 $(X,Y)$ 服从二维正态分布 $N({\mu }_{1},{\mu }_{2};{{\sigma }_{1}}^{2},{{\sigma }_{2}}^{2};\rho )$,其联合密度函数为:
$$
f(x,y) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1-\rho^2)}\left[\left(\frac{x-\mu_1}{\sigma_1}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right) + \left(\frac{y-\mu_2}{\sigma_2}\right)^2\right]\right)
$$
步骤 2:求边缘密度函数
为了证明 $X\sim N({\mu }_{1},{{\sigma }_{1}}^{2})$,我们需要计算 $X$ 的边缘密度函数 $f_X(x)$,即对联合密度函数 $f(x,y)$ 关于 $y$ 进行积分:
$$
f_X(x) = \int_{-\infty}^{+\infty} f(x,y) dy
$$
将联合密度函数代入上式,我们得到:
$$
f_X(x) = \int_{-\infty}^{+\infty} \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1-\rho^2)}\left[\left(\frac{x-\mu_1}{\sigma_1}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right) + \left(\frac{y-\mu_2}{\sigma_2}\right)^2\right]\right) dy
$$
注意到积分中的指数部分可以重新组织为一个关于 $y$ 的二次函数,其形式为:
$$
\left(\frac{y-\mu_2}{\sigma_2}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right)
$$
这个二次函数的积分结果是一个标准正态分布的积分形式,其结果为:
$$
f_X(x) = \frac{1}{\sqrt{2\pi}\sigma_1}\exp\left(-\frac{(x-\mu_1)^2}{2\sigma_1^2}\right)
$$
这表明 $X$ 服从正态分布 $N(\mu_1, \sigma_1^2)$。
步骤 3:证明 $Y$ 的分布
同理,为了证明 $Y\sim N({\mu }_{2},{{\sigma }_{2}}^{2})$,我们需要计算 $Y$ 的边缘密度函数 $f_Y(y)$,即对联合密度函数 $f(x,y)$ 关于 $x$ 进行积分:
$$
f_Y(y) = \int_{-\infty}^{+\infty} f(x,y) dx
$$
将联合密度函数代入上式,我们得到:
$$
f_Y(y) = \int_{-\infty}^{+\infty} \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1-\rho^2)}\left[\left(\frac{x-\mu_1}{\sigma_1}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right) + \left(\frac{y-\mu_2}{\sigma_2}\right)^2\right]\right) dx
$$
注意到积分中的指数部分可以重新组织为一个关于 $x$ 的二次函数,其形式为:
$$
\left(\frac{x-\mu_1}{\sigma_1}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right)
$$
这个二次函数的积分结果是一个标准正态分布的积分形式,其结果为:
$$
f_Y(y) = \frac{1}{\sqrt{2\pi}\sigma_2}\exp\left(-\frac{(y-\mu_2)^2}{2\sigma_2^2}\right)
$$
这表明 $Y$ 服从正态分布 $N(\mu_2, \sigma_2^2)$。
二维随机变量 $(X,Y)$ 服从二维正态分布 $N({\mu }_{1},{\mu }_{2};{{\sigma }_{1}}^{2},{{\sigma }_{2}}^{2};\rho )$,其联合密度函数为:
$$
f(x,y) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1-\rho^2)}\left[\left(\frac{x-\mu_1}{\sigma_1}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right) + \left(\frac{y-\mu_2}{\sigma_2}\right)^2\right]\right)
$$
步骤 2:求边缘密度函数
为了证明 $X\sim N({\mu }_{1},{{\sigma }_{1}}^{2})$,我们需要计算 $X$ 的边缘密度函数 $f_X(x)$,即对联合密度函数 $f(x,y)$ 关于 $y$ 进行积分:
$$
f_X(x) = \int_{-\infty}^{+\infty} f(x,y) dy
$$
将联合密度函数代入上式,我们得到:
$$
f_X(x) = \int_{-\infty}^{+\infty} \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1-\rho^2)}\left[\left(\frac{x-\mu_1}{\sigma_1}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right) + \left(\frac{y-\mu_2}{\sigma_2}\right)^2\right]\right) dy
$$
注意到积分中的指数部分可以重新组织为一个关于 $y$ 的二次函数,其形式为:
$$
\left(\frac{y-\mu_2}{\sigma_2}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right)
$$
这个二次函数的积分结果是一个标准正态分布的积分形式,其结果为:
$$
f_X(x) = \frac{1}{\sqrt{2\pi}\sigma_1}\exp\left(-\frac{(x-\mu_1)^2}{2\sigma_1^2}\right)
$$
这表明 $X$ 服从正态分布 $N(\mu_1, \sigma_1^2)$。
步骤 3:证明 $Y$ 的分布
同理,为了证明 $Y\sim N({\mu }_{2},{{\sigma }_{2}}^{2})$,我们需要计算 $Y$ 的边缘密度函数 $f_Y(y)$,即对联合密度函数 $f(x,y)$ 关于 $x$ 进行积分:
$$
f_Y(y) = \int_{-\infty}^{+\infty} f(x,y) dx
$$
将联合密度函数代入上式,我们得到:
$$
f_Y(y) = \int_{-\infty}^{+\infty} \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1-\rho^2)}\left[\left(\frac{x-\mu_1}{\sigma_1}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right) + \left(\frac{y-\mu_2}{\sigma_2}\right)^2\right]\right) dx
$$
注意到积分中的指数部分可以重新组织为一个关于 $x$ 的二次函数,其形式为:
$$
\left(\frac{x-\mu_1}{\sigma_1}\right)^2 - 2\rho\left(\frac{x-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right)
$$
这个二次函数的积分结果是一个标准正态分布的积分形式,其结果为:
$$
f_Y(y) = \frac{1}{\sqrt{2\pi}\sigma_2}\exp\left(-\frac{(y-\mu_2)^2}{2\sigma_2^2}\right)
$$
这表明 $Y$ 服从正态分布 $N(\mu_2, \sigma_2^2)$。